Мы принимаем к оплате:
«Подарочный сертификат» от нашего Учебного Центра – это лучший подарок для тех, кто Вам дорог! Оплате обучение и подарите Вашим родным и близким обучение по любому из курсов!!!
«Сертификат на повторное обучение» дает возможность повторно пройти обучение в нашем Учебном Центре со скидкой 1000 рублей!
А также:
Построение разверток в автокаде
Развертка конуса
Выполним одно из простых, но часто используемых в черчении построений – построим развертку конуса (боковой поверхности). В Autocad есть средства, позволяющие быстро и точно решать подобные задачи.
1. Для начала вспомним школьный курс геометрии:
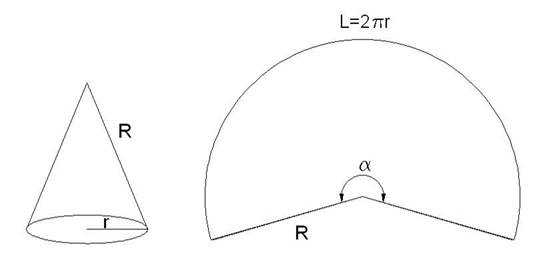
Развертка боковой поверхности прямого конуса – это сектор круга, радиус которого равен образующей конуса R, а длина дуги L=2?r, где r – радиус основания конуса. Угол ? в градусах равен 360 * 2? r/2?R = 360r/R.
2. Пусть конус задан графически в виде треугольника (для твердотельного конуса построение также справедливо):
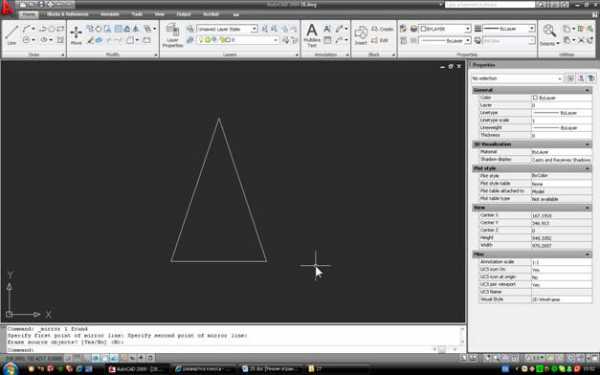
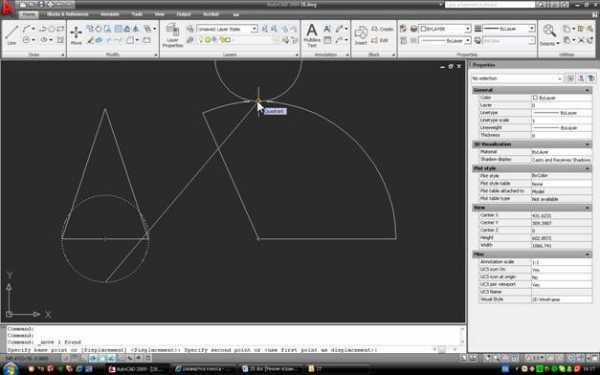
Построим его развертку. Вариантов такого построения очень много, мы же применим способ, который не требует сторонних расчетов и использует только инструменты Autocad. Сначала построим произвольную дугу с радиусом R. Для этого начертим окружность, используя образующую конуса в качестве радиуса:
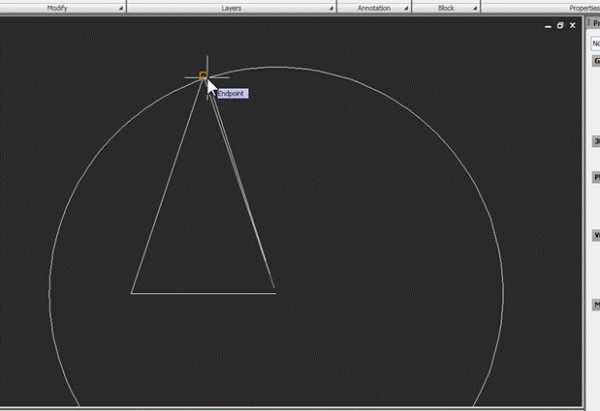
Затем командой Trim отсечем от нее любую часть, чтобы она превратилась в дугу. В качестве режущей кромки используем произвольную вспомогательную линию:
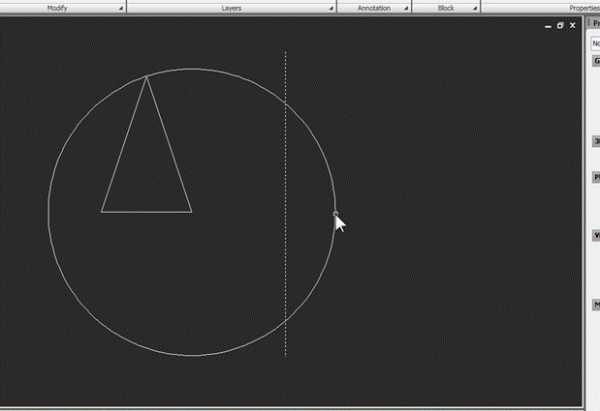
Затем линию удаляем, выделяем дугу и открываем окно свойств:
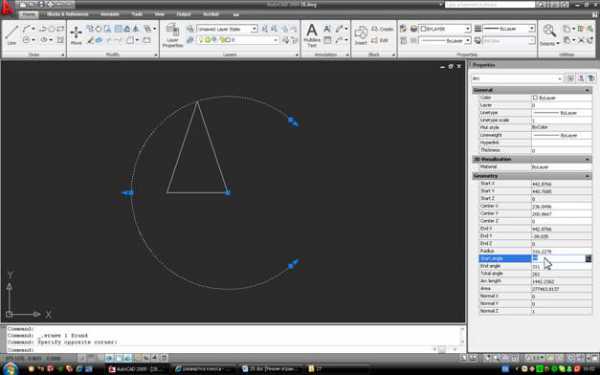
Изменяем Start angle – устанавливаем его в 0. Затем в окошке End angle нажимаем значок встроенного калькулятора:
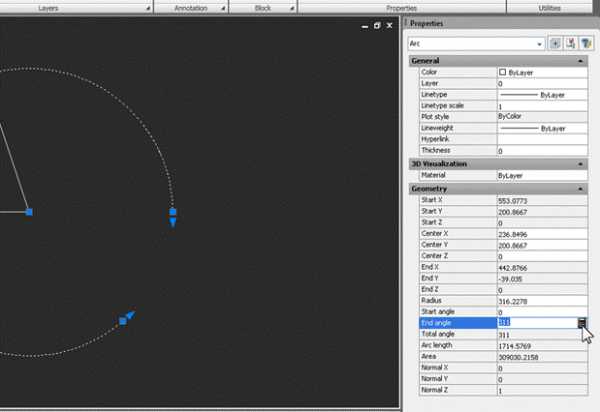
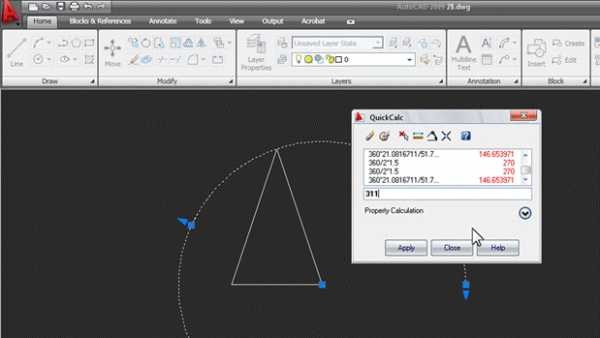
В появившемся окне «вычисляем» угол. Набираем с клавиатуры 360* и жмем кнопку с линейкой:
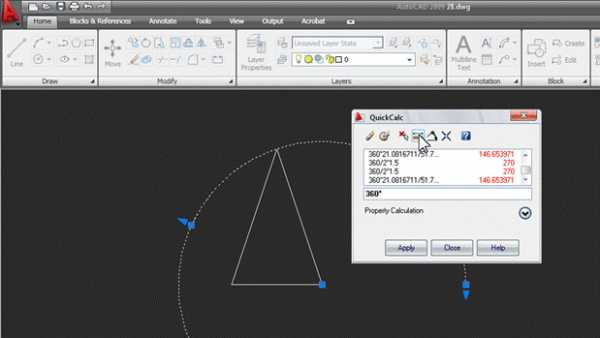
Указываем на экране радиус основания конуса двумя точками (середина основания и нижняя вершина треугольника). Затем c клавиатуры вводим знак деления / и таким же образом указываем длину образующей конуса. В итоге в окне появляется выражение с параметрами вашего конуса:
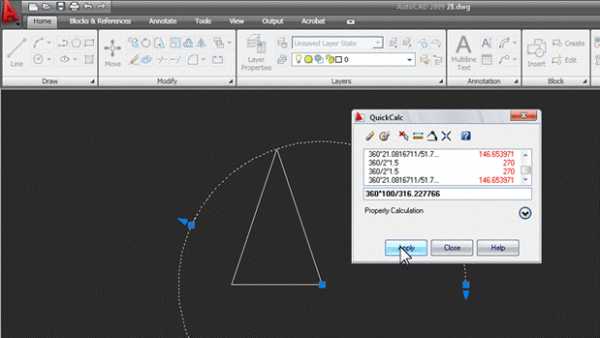
Жмем Apply, и угол автоматически вычисляется и присваивается свойству End angle:
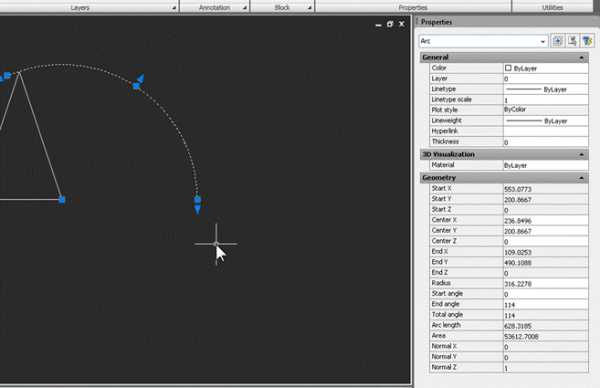
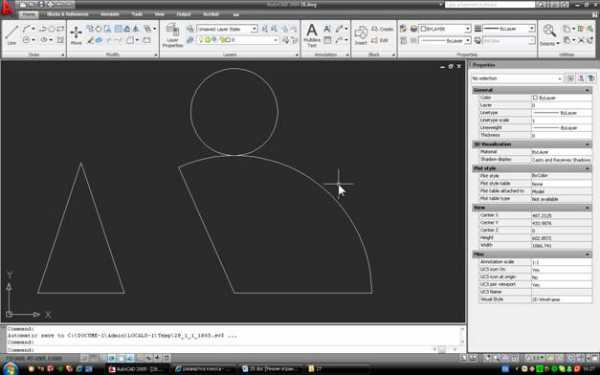
3. Построим основание конуса, чтобы развертка стала полной, и проверим правильность построений. Строим окружность на основании треугольника, как на диаметре, и переносим ее так, чтобы она касалась наружной дуги развертки:
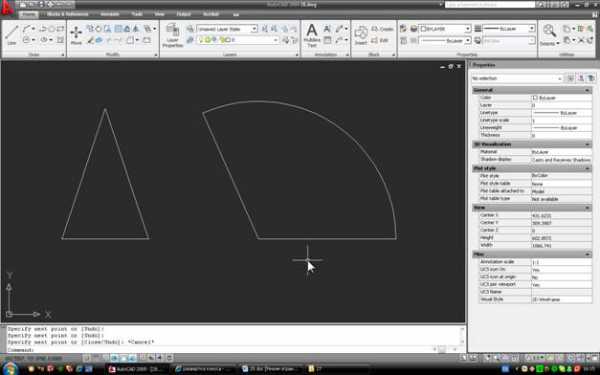
Вот готовая развертка:
Теперь, если по очереди выделить окружность-основание и дугу, можно в свойствах сравнить их длины. У окружности это свойство называется Circumference, у дуги – Arc length:
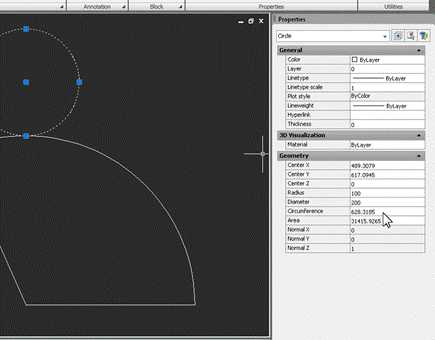
Если построения выполнены правильно, числа должны совпасть.
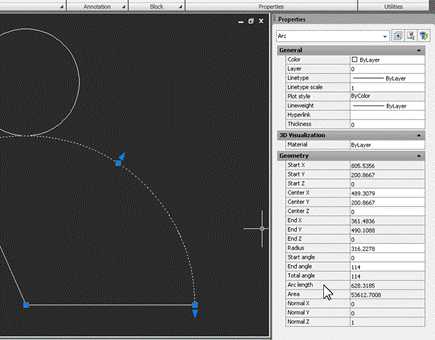
Как видим, строить развертку конуса (как и многих других геометрических тел) в Autocad гораздо проще, чем на бумаге.
Построение разверток и 3D-моделей
Комментарии 1-15 из 23
Спасибо большое за прогу -очень помогла.Правда по началу не очень разобрался с кряком и когда сохранял -сохранил не как полилинию,а как векторы -но после проб и ошибок ща все замечательно.
Большое спасибо. это программа очень мне помогла
Спасибо огромное!!!
А в архиве вирус Panda находит
Для Sergey PNS попробуй экспорт прямо в АвтоКАД. есть такой пункт в меню и все работает тип-топ и без разрыва контура. На компе должен стоять АвтоКАД 2000 или 2002. А экспорт в файл формата *.dxf у меня тоже работает с глюками на этой версии.
Всем привет!!! Люди я работаю на заводе по вентиляции прога конечно классная но: 1. кода я экспорт делаю то у меня контуры разорвоны.2. или ломаные а станок(плазма) режет ломанно
Подскажите пожалуйста как апгрейдить прогу с ихнего сайта
А в 2004 работает? Спасибо заранее за ответ
Спасибо огромное, прога - вещь( ну, это не к вам, конечно:)), а за то, что она работает - спасибо. Аещё какие-нибудь библиотеки к ней существуют?
поскажите где выдаёт это прога размеры развёртки
Всё нормально работает, погрешнось с другими прогами +-1 мм испытали в натурных условиях - всё совпало чётко!!!
Thank you very muhc
В архиве версия 3.3.3 от 2002-01-20. Работает с AutoCAD 2002. Прямые ссылки на современную версию: версия 3.9.9x (5 301 979 bytes) от 2006-01-10 на http://www.plate-n-sheet.com/download/PnS3_English.zip версия 3.9.9f (5 275 010 bytes) от 2005-01-23 на http://www.asvic.com.au/ftp/PlateNSheet.exe версия 3.9.9d (4 888 605 bytes) от 2004-11-09 на http://www.rlcad.com.au/Download/PlateNSheet_Pro.zip но это только демо-версиии (This program is running in evalution mode). За активацию Вам предложат заплатить 700 денег США.Предыдущее сообщение, подписанное ником MEXSOFT, скорее всего ошибка или розыгрыш.
Установил апгрейд с их сайта по верх скачанного, все работает
No Ivan/ После генерации кода авторизации Кейгеном из нового файла ReadMe прога заработала нормально: построение любой фигуры и экспорт в Автокад2002 как в формате *.dxf так и *.dwg.Распечатка из проги не получается, и по моему мнению, это не беда, т.к. в Автокаде можно сформировать нормальный лист с объемным изображением и развертками любого объекта.
325113251032509325083250732506325053250432503325023250132500324993249832497
Развертка конуса. Урок.
Anton Dmz 04.05.2011Выполним одно из простых, но часто используемых в черчении построений – построим развертку боковой поверхности конуса. В Autocad есть средства, позволяющие быстро и точно решать подобные задачи.
Выполним одно из простых, но часто используемых в черчении построений – построим развертку боковой поверхности конуса. В Autocad есть средства, позволяющие быстро и точно решать подобные задачи.1. Для начала вспомним школьный курс геометрии:
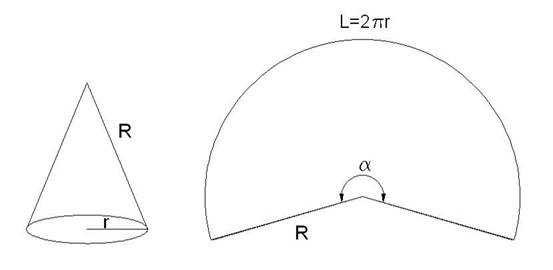
Развертка боковой поверхности прямого конуса – это сектор круга, радиус которого равен образующей конуса R, а длина дуги L=2?r, где r – радиус основания конуса. Угол ? в градусах равен 360 * 2? r/2?R = 360r/R.
2. Пусть конус задан графически в виде треугольника (для твердотельного конуса построение также справедливо):
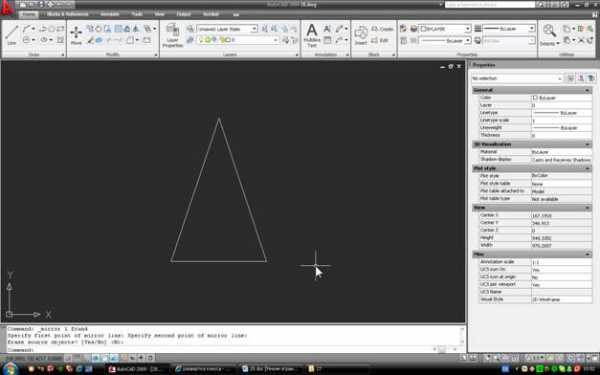
Построим его развертку. Вариантов такого построения очень много, мы же применим способ, который не требует сторонних расчетов и использует только инструменты Autocad. Сначала построим произвольную дугу с радиусом R. Для этого начертим окружность, используя образующую конуса в качестве радиуса:
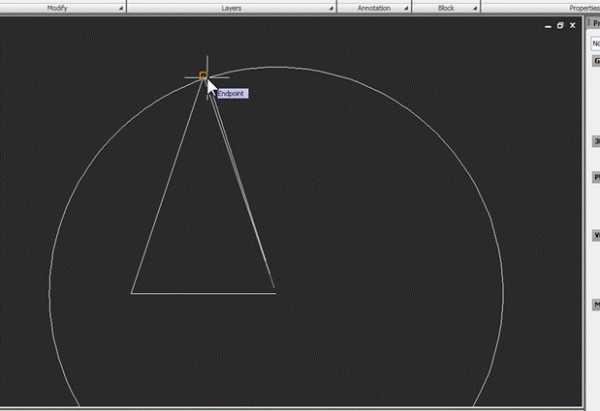
Затем командой Trim отсечем от нее любую часть, чтобы она превратилась в дугу. В качестве режущей кромки используем произвольную вспомогательную линию:
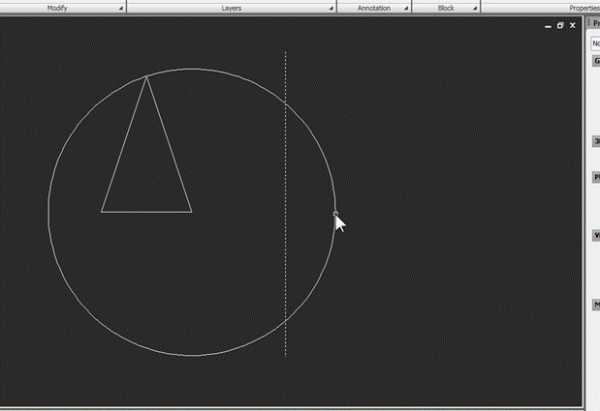
Затем линию удаляем, выделяем дугу и открываем окно свойств:
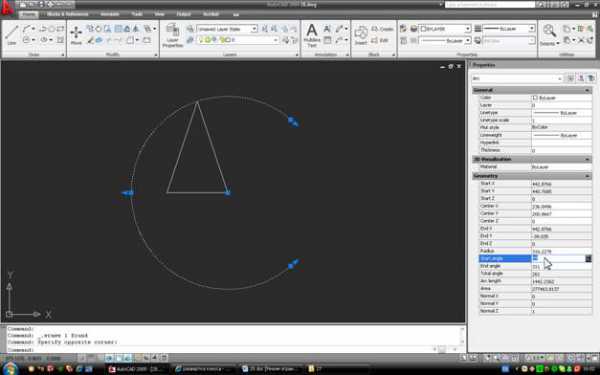
Изменяем Start angle – устанавливаем его в 0. Затем в окошке End angle нажимаем значок встроенного калькулятора:
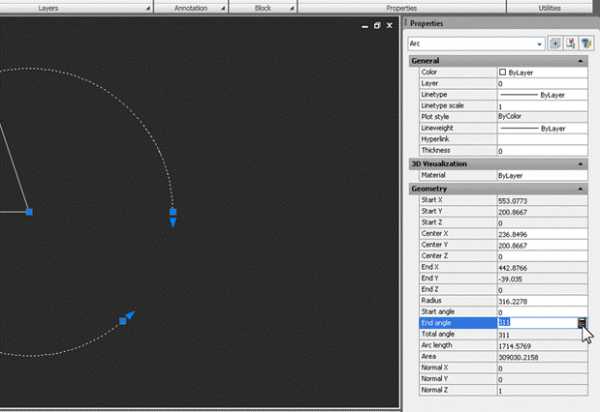
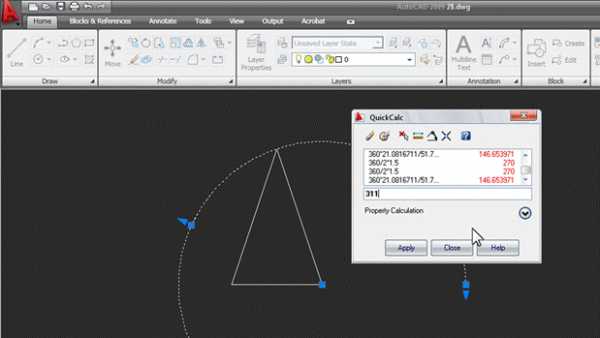
В появившемся окне «вычисляем» угол. Набираем с клавиатуры 360* и жмем кнопку с линейкой:
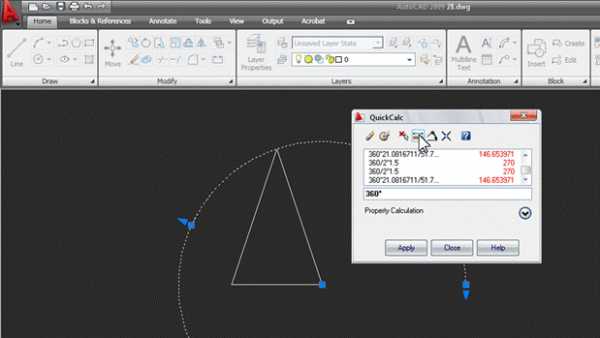
Указываем на экране радиус основания конуса двумя точками (середина основания и нижняя вершина треугольника). Затем c клавиатуры вводим знак деления / и таким же образом указываем длину образующей конуса. В итоге в окне появляется выражение с параметрами вашего конуса:
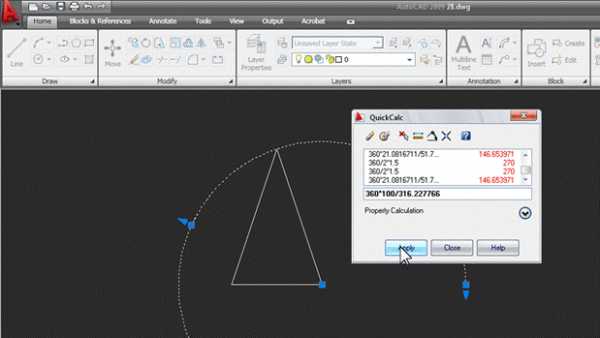
Жмем Apply, и угол автоматически вычисляется и присваивается свойству End angle:
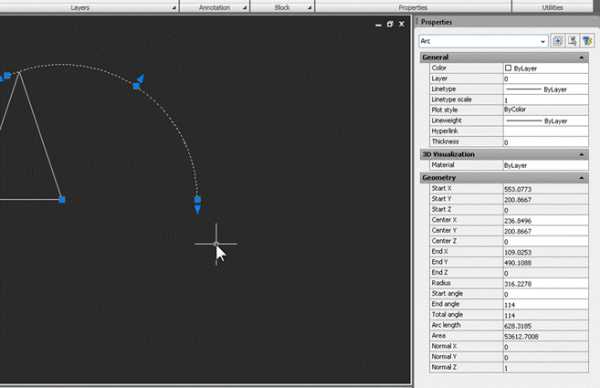
3. Построим основание конуса, чтобы развертка стала полной, и проверим правильность построений. Строим окружность на основании треугольника, как на диаметре, и переносим ее так, чтобы она касалась наружной дуги развертки:
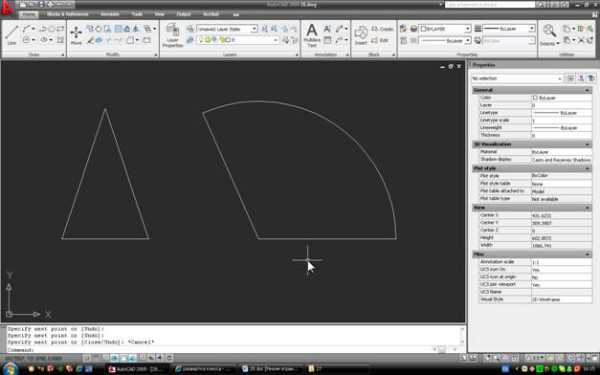
Вот готовая развертка:
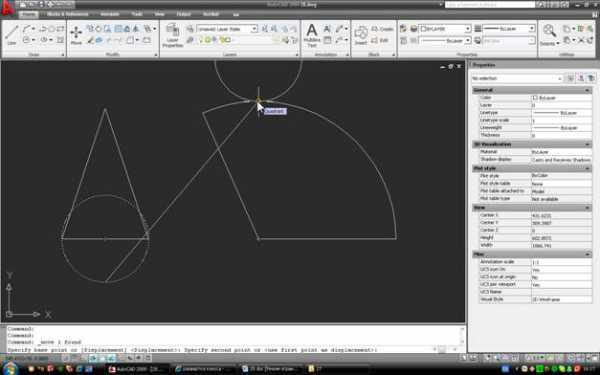
Теперь, если по очереди выделить окружность-основание и дугу, можно в свойствах сравнить их длины. У окружности это свойство называется Circumference, у дуги – Arc length:
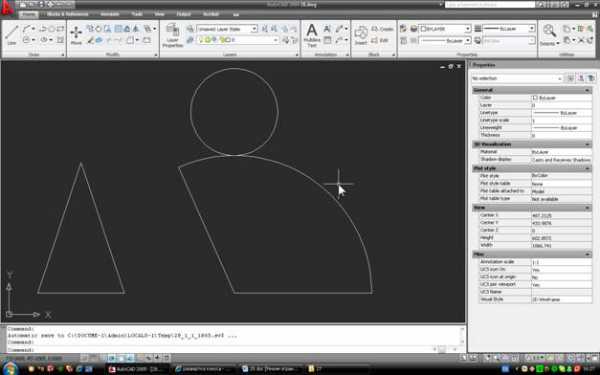
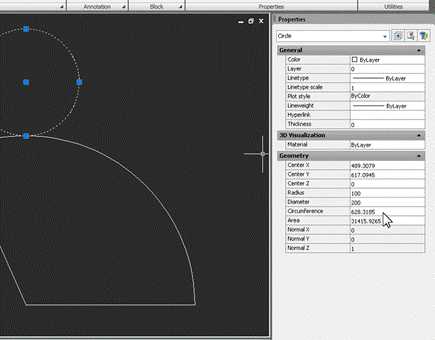
Если построения выполнены правильно, числа должны совпасть.
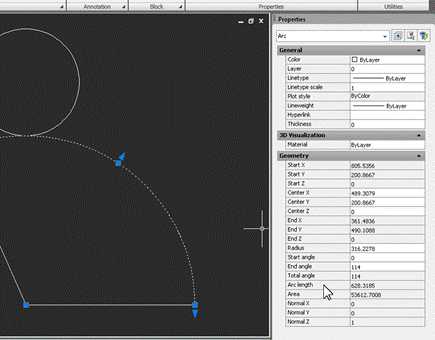
Как видим, строить развертку конуса (как и многих других геометрических тел) в Autocad гораздо проще, чем на бумаге.
Источник: http://autocad-lessons.ruСтудия Vertex. Только качественные уроки AutoCAD.
Развертки цилиндрических поверхностей в программе AutoCAD
УДК 515. 2:681.3
РАЗВЕРТКИ ЦИЛИНДРИЧЕСКИХ ПОВЕРХНОСТЕЙ В ПРОГРАММЕ А^оСАй
Н.Ю. Смекаева, Е.В. Шамрай-Лемешко; Дальрыбвтуз, Владивосток
Описаны примеры построения некоторых цилиндрических поверхностей в современном исполнении в программе АШоСАй. Такие поверхности встречаются при изготовлении воздуховодов, вентиляционных систем, водосточных труб и др.
Технические развертки изделий, содержащие элементы цилиндрических поверхностей, широко используются при изготовлении воздуховодов, вентиляционных систем, водосточных труб и труб пневматического транспорта. В этих изделиях цилиндры обычно пересечены плоскостью, наклонной к образующим. В данной работе рассмотрены примеры построения разверток цилиндров вращения в современном исполнении в программе А^оСАй.
Цилиндрические поверхности относятся к развертываемым поверхностям, т.е. в общем случае их развертки строят как развертки гранных поверхностей, вписанных или описанных около них.
При построении разверток цилиндров вращения не требуется аппроксимации их гранными поверхностями, так как между параметрами их поверхностей и их развертками существуют простые аналитические зависимости. Ниже рассмотрены примеры построения разверток наиболее часто встречающихся случаев цилиндрических поверхностей вращения.
Развертка отсека цилиндрической поверхности вращения (рис. 1)
В общем случае построение развертки такой поверхности состоит в том, что в нее вписывают призматическую поверхность и строят ее развертку. Процесс развертывания поверхности состоит в спрямлении и изгибании принадлежащих ей кривых. Так как с помощью циркуля и линейки точное спрямление невозможно, развертывание поверхности выполняется приближенно [1]. Рассмотрим поверхность на рис 1.
Из чертежа видно, что образующие цилиндрического отсека -горизонтально проецирующие прямые, т.е. их фронтальные проекции -натуральные величины. Направляющая поверхности принадлежит горизонтальной плоскости уровня, т.е. проецируется на плоскость П1 в натуральную величину.
Для построения приближенной развертки данной поверхности впишем в нее трехгранную призматическую поверхность. Ее развертка будет приближенной разверткой данной поверхности. Направляющую линию аппроксимируем (заменяем) вписанной ломаной линией: для этого командой ТОЧКА разделим дугу на неравные части. Точки деления 11, 21, З1, 41 выбираем так, чтобы длины хорд мало отличались от длин дуг. Находим фронтальные проекции этих точек и из них проводим образующие 1212, 2222 и др. Развертку строим справа от фронтальной проекции поверхности.
Командой ОТРЕЗОК проводим горизонтальную линию от точек нижнего основания на П2. На этой прямой от точки 1о откладываем отрезки 1о2о = 1і2і, 2о3о = 2о3о и 3о4о = 3і4і КОПИРУЙ, ПЕРЕНЕСИ, ПОВЕРНИ, взяв их величины на Пі [2].
Натуральные величины хорд можно определить более точно и быстрее командой РАЗМЕРЫ ЛИНЕЙНЫЕ (рис. 1, а) и отложить их числовые значения от точки 1о (рис. 1, а).
Из точек 1 о, 2о, 3о и 4о восстановим перпендикуляры командой ОТРЕЗОК. На них отложим образующие цилиндрической поверхности. Размеры образующих переносим горизонтальными линиями с фронтальной проекции. Полученные точки соединяем плавной кривой (команда ДУГА) [1].
Построить развертку боковой поверхности цилиндра вращения прямого кругового цилиндра (рис. 2)
Для построения развертки цилиндра вращения нет необходимости вписывать в него многогранник, так как существует аналитическая зависимость между параметрами поверхности цилиндра и развертки.
■I о , а 1
Рис. 2. Развертка поверхности цилиндра вращения
Боковая развертка поверхности такого цилиндра представляет собой прямоугольник, высота которого равна высоте цилиндра, а ширина
- длине окружности основания цилиндра
^ = 2жЯ,
где Я - радиус окружности основания цилиндра.
Построение начинаем с проведения горизонтальной линии от нижнего основания справа от фронтальной проекции. Выбираем точку 1о, от нее откладываем длину окружности основания цилиндра
I- = 2ж Я = 2- 3,14- 20 = 125,6.
При построении развертки используем режим ОРТО, команду ОТРЕЗОК и шаговую привязку.
Из концов отрезка восстановим перпендикуляры, равные образующей цилиндра - 55 мм, и обведем прямоугольник контурной линией.
Для построения на развертке точки М определим длину дуги 1121
- = 2жRa / 360°.
Определим угол дуги командой РАЗМЕРЫ УГЛОВЫЕ, а = 120. Длина дуги 1121 = 41,7 мм. Отложим этот размер от точки 1о. Дальнейшее построение ясно из чертежа (см. рис. 2).
Построить развертку поверхности кругового цилиндра с отверстием 0 22 мм
Развертку цилиндра строим как в предыдущем примере -прямоугольником, а линия окружности (отверстие) изобразится на развертке в виде замкнутой кривой. Поверхность имеет фронтальную плоскость симметрии, а отверстие в продольном направлении может располагаться в любом месте развертки. Поэтому построим левую половину цилиндра с половиной отверстия, которое расположим по середине. Полный контур развертки с отверстием получим командой ЗЕРКАЛО.
Чтобы развернуть половину цилиндра, вычисляем длину нижнего основания и развертываем его половину прямую линию.
Для нанесения кривой на развертке выполним следующие построения.
Вначале на поверхности цилиндра командой ОТРЕЗОК проведем на фронтальной проекции две образующие - касательную в точке 4 и через диаметр (точки 1 и 2 на рис.3, б) [1].
Построим эти точки на развертке. Построение точек 1 и 2 видно из чертежа (рис.3, а). Образующую, на которой лежит точка 4, найдем, замерив дугу от точки 1 до точки 4 на горизонтальной проекции. Для построения точек 3 и 5 проведем произвольную образующую на фронтальной проекции, построим ее на развертке подобно точке 4 (рис.3, б).
Полученные точки соединим плавной кривой (команда ДУГА). Полный контур развертки поверхности цилиндра с круговым отверстием получим командой ЗЕРКАЛО (рис. 3, в) [2].
Развертка поверхности цилиндра вращения, усеченного плоскостью
Развертка этого цилиндра (рис. 4) состоит из двух частей: нижняя часть развернута в прямоугольник с высотой 11 и основанием, равным длине окружности. Верхняя часть развертки ограничена кривой линией. Цилиндр имеет фронтальную плоскость симметрии, поэтому построим половину развертки. Полную развертку получим командой ЗЕРКАЛО [2].
Построение начинаем слева от фронтальной проекции. Командой отрезок проводим горизонтальную линию от нижнего основания и отложим половину длины окружности DП/2 и высоту 11.
Боковую развертку верхней части строим следующим образом.
Командой МАССИВ разделим полуокружность на горизонтальной проекции на 6 частей. Командой ОТРЕЗОК построим образующие на плоскости П2. Таким же образом разделим длину полуокружности на развертке и восставим перпендикуляры из точек деления, они определят положение образующих цилиндра. Размеры образующих перенесем с фронтальной проекции командой ОТРЕЗОК.
Полученные точки соединим плавной кривой (командой ДУГА). Эта кривая является синусоидой [1].
Построения верхнего и нижнего оснований видно из чертежа.
Рис. 4. Развертка усеченного цилиндра вращения
Представленная на рис. 4 развертка построена в предположении, что поверхность данного цилиндра разрезана вдоль наименьшей образующей. Можно разрезать поверхность вдоль какой-либо другой образующей, в том числе, вдоль наибольшей. С геометрической точки зрения такие развертки равноценны. Выбор наиболее целесообразного варианта зависит от принятой технологии изготовления.
Библиографический список
1. Высоцкая Н.Н. и др. Технические развертки изделий из листового материала. Л.: Машиностроение, 1968.
2. Красновский Д.Г. AutoCAD для всех. М., 1990.